
If you drop a perpendicular line from the ridge, you get two congruent right triangles. The gable end of a roof is an isosceles triangle. Using the angle and the opposite side, use tangent to find the adjacent side.ġ89. You know the angle (again, the angle of elevation) and the adjacent side (the distance to the steeple), so use tangents to find the opposite side.ġ53. You know the adjacent side (the distance to the tree), and you know the angle (the angle of elevation), so you can use tangents to find the height of the tree.ġ52. Remember that the tangent of an angle in a right triangle is the opposite side divided by the adjacent side. Then you’ll have to solve a quadratic equation.ġ51. Second, the Pythagorean identity, sin 2 t + cos 2 t = 1. You can then determine c by the Pythagorean theorem, or by using sines, or by using cosines.Ĥ9.
Since you know a and tan A, you can find b. Hints A general hint for all these exercises is to draw the figure first.Ģ9. The gable end of a roof measures 40 feet across at the base and 26 feet from the base to the ridge. Find how much the height of the second hill exceeds that of the first.ġ89. From one hill to the top of another distant 6290 feet has an angle of elevation of 4° 9'. From one hill the top of another 128 feet higher has an angle of elevation of 2° 40'. On one side of a stream a pole 50 feet high has from an opposite point an angle of elevation of 5° 33'. Find the height of a tower, distant 186 feet, angle of elevation 40° 44'.ġ60. From the top of a lighthouse 165 feet above the water the angle of depression of a ship is 3° 50'. From a ship, the angle of elevation of the top of a lighthouse 200 feet above the water is 2° 20'. Find the height of a steeple distant 321 feet, angle of elevation 35 ° 16'.ġ53. The angle of elevation of a tree 250 feet distant is 16° 13'. In problems involving the shadow of an object the shadow is supposed to fall on the horizontal plane through the base of the object, unless otherwise stated.ġ51. The height of the observer’s eye is not to be taken into account unless specially mentioned. Note: In the following problems distance means horizontal distance, unless otherwise stated the height of an object means its height above the horizontal plane through the point of observation. In a right triangle a = 30 yards and tan A = 2. It may be better to say that the tangent of 90° is undefined since, using the circle definition, the ray out from the origin at 90° never meets the tangent line.Ģ9. That’s because as the angle grows toward 90°, it’s tangent grows without bound. Note that the tangent of a right angle is listed as infinity. The ratios are the values of the trig functions. You don’t have to remember all this information if you can just remember the ratios of the sides of a 45°-45°-90° triangle and a 30°-60°-90° triangle.

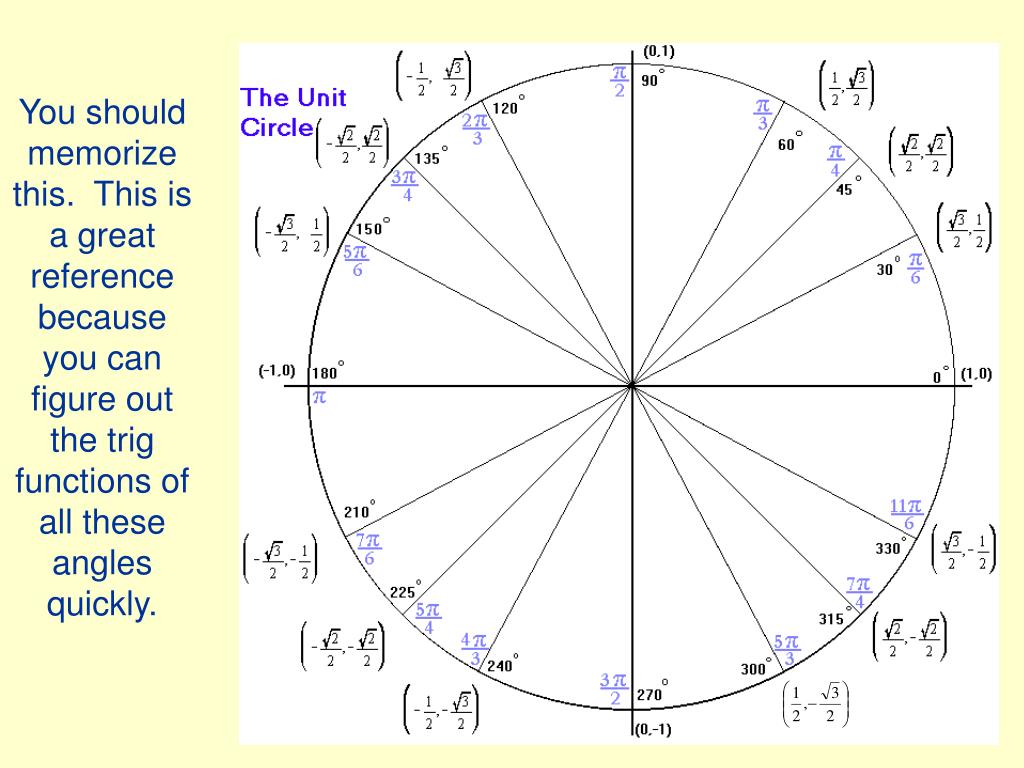
We can extend our table of sines and cosines of common angles to tangents. Tangents are frequently used to solve problems involving angles of elevation and depression.
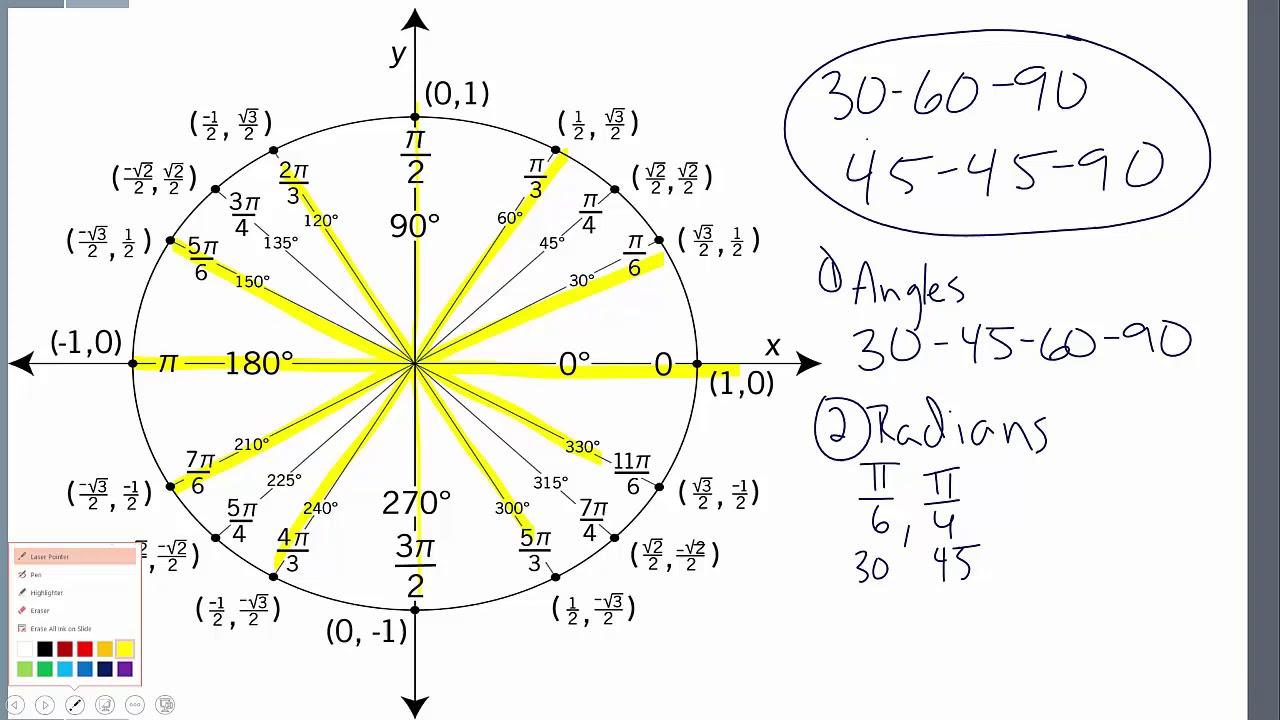
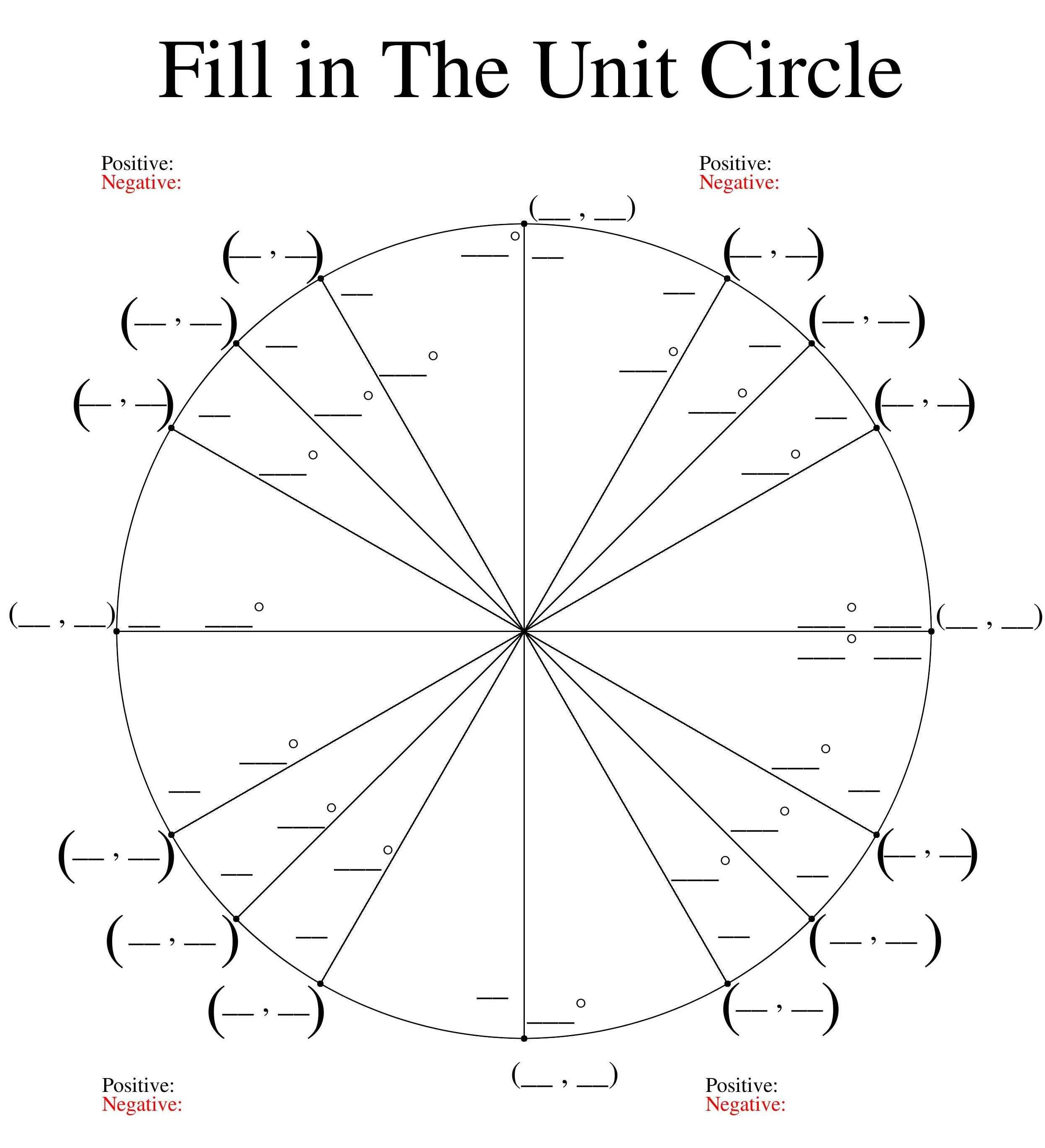
Likewise, the “angle of depression” to a point C below the horizon is the angle CAH. If you’re at point A, and AH is a horizontal line, then the angle of elevation to a point B above the horizon is the angle BAH. If you are to ever be tested on this, make a quick sketch of the first quadrant of the circle, and remember the pattern that underlies the unit circle.The term “angle of elevation” refers to the angle above the horizontal from the viewer. Take a look at the ones with the same denominator and see if you can correspond any patterns to what you see. Certain radian values are simply reflections of the other.S i n e : sin ( α ) = y c o s i n e : cos ( α ) = x.


 0 kommentar(er)
0 kommentar(er)
